Experiments with implementing a convolutional neural network (CNN) in NumPy.
Written by David Stein (david@djstein.com). See FAQ.html for more information.
Also available at https://www.github.com/neuron-whisperer/cnn-numpy.
The purpose of this project is to provide a fully working, NumPy-only implementation of a convolutional neural network, with a few goals:
Presenting the simplest, cleanest example of a fully implemented, working CNN as a minimal adaptation of Dr. Andrew Ng's example code. See: cnn_numpy.py.
Provide a working application of the above example to classify the MNIST database of handwritten digits. See: mnist.py.
While these two efforts were successful, it happens that the example code runs prohibitively slowly - because it is designed for clarity and education, not actual use. It is not possible to train the model to do anything meaningful in a reasonable amount of time. Thus, the following objectives were added:
cnn_numpy_sg.py.Convolutional neural networks are the current primary model of deep learning for tasks such as image analysis. Dr. Andrew Ng, one of the contemporary experts in machine learning, offers this excellent Coursera course on convolutional neural networks that includes an assignment entitled "Build a Convolutional Neural Network Step by Step."
The assignment is presented as a Jupyter notebook with NumPy-based code and a detailed explanation of the calculations, including helpful illustrations. The code includes a convolutional layer, a MaxPool layer, and an AvgPool layer. The Jupyter notebook also includes unit tests to show that the individual functions work.
However, the code in the Jupyter notebook has a few issues that prevent its use for anything beyond the confines of the assignment:
The code is a bit... primitive. It is structured as a set of global functions. Parameters are passed in a "cache" dictionary, with names identified by strings. Some variables are cached and then never used. Different variable names are sometimes used between a calling function and a called function. Tracing the interconnection of the functions is rather painful due to big chunks of explanatory text, unit tests, and output.
The implementation in the Jupyter notebook is not complete! The convolutional layers calculate dW/db, but do not update the filters. The implementations do not include a fully connected layer - these are developed in previous exercises - nor a flattening layer (which is trivial to implement, but its absence is frustrating).
The implementation in the Jupyter notebook is not applied to any kind of problem. It is simply presented as an example. The next exercise in the course sequence involves applying a CNN to the MNIST handwritten digits data set - and yet, it does not use the CNN implementation from this assignment; instead, it switches to a pure TensorFlow implementation. (To make matters worse, the TensorFlow implementation requires TensorFlow 1.x, which will of course not run in the current TensorFlow 2.x environment!)
These limitations create two problems.
Problem #1: While reviewing "Build a Convolutional Neural Network Step by Step," it is very difficult to take a step back and see a fully-realized CNN that uses this code, including training. It is also disappointing that the code is not shown to run against any kind of sample problem. Students cannot easily see it in action. Students cannot experiment with the structure or hyperparameters to see how performance may differ. And students cannot easily apply this code to other standard data sets to develop any kind of skill and confidence in this knowledge.
(As an avid student of machine learning, I am continually irked by the gap between the skill set of theoretical knowledge, such as how models work, and the skill set of applied machine learning, such as the available platforms and the common theories of how to use them. Anything that can be done to bridge this gap with actual knowledge will, I believe, be helpful for promoting a comprehensive understanding of the field.)
Based on the above, I set out fill in the gaps. I sought to refactor, streamline, and just generally normalize all of Dr. Ng's code into a tight, cohesive CNN library - one that faithfully reproduces the algorithms from the example code, but in a much more readable, usable way. Also, I sought to apply this model to the MNIST database in order to show that it works. The result of this effort is cnn_numpy.py and mnist.py:
cnn_numpy.py is a 180-line file that includes:
A ConvLayer class
A PoolLayer base class, with PoolLayer_Max and AvgPoolLayer_Avg subclasses
A FlatLayer class
An FCLayer base class, with FCLayer_ReLU, FCLayer_Sigmoid, and FCLayer_Softmax subclasses
A Network class with predict(), evaluate(), and train() functions, based on categorical cross-entropy and multiclass error, and a parameterized learning rate
And mnist.py is an 80-line file that loads the MNIST handwritten digits data set from Dr. Yann LeCun's website, unpacks it, and trains any combination of layers from cnn_numpy.py to perform multiclass classification. Students may freely experiment with different architectures by changing one line of code, like this non-CNN ("flat") model:
net = Network([FlatLayer(), FCLayer_ReLU(100), FCLayer_Softmax(10)])
...or this CNN model:
net = Network([ConvLayer(32, 3), PoolLayer_Max(2, 2), FlatLayer(), FCLayer_ReLU(100), FCLayer_Softmax(10)])
This is a TensorFlow-like syntax, but unlike TensorFlow, cnn_numpy.py is completely transparent and readable.
For convenience, mnist.py allows you to select either architecture with a suitable set of training parameters:
python3 mnist.py flat naive
python3 mnist.py cnn naive
The flat architecture work great. On a typical machine, it can train from scratch with a 95% training split of the data set to reach a classification error under 10% within one minute, and under 5% in three minutes.
The CNN architectures also runs... slowly. Brutally slowly. Unusably slowly.
Problem #2: The code from "Build a Convolutional Neural Network Step by Step" is prohibitively slow. So slow that it is not realistically possible to apply it to a problem or to see it learn anything. Thus, it is difficult to see that it even works, let alone experiment with it.
The ConvLayer and PoolLayer classes require a four-layer-deep loop in Python for each of the forward and backward passes. The loop iterates over: (1) The inputs in the input tensor, (2) the height of each input, (3) the width of each input, and (4) each filter in the convolutional layer.
As a result of this deeply nested iteration, processing one epoch of the MNIST data set with a one-ConvLayer CNN with 32 filters would require 28 trillion NumPy calculations. NumPy is indeed fast, but executing literally trillions of small NumPy calculations requires an absurdly long period of time.
I suppose that these factors explain the hard transition in the CNN course sequence from the NumPy-based "Build a Convolutional Neural Network Step by Step" code to the TensorFlow-based code for the immediately following lesson. But it does feel like a bait-and-switch: "Here is some code... now that we've developed all of that, let's use none of it, and instead switch to a totally different platform."
The challenge presented at this stage is: How can the examples of pooling and convolutional layers from "Build a Convolutional Neural Network Step by Step" be modified to use the same model, and only simple NumPy, but to make much better use of NumPy's array processing capabilities so that iteration can be vastly reduced?
NumPy is capable of performing operations on large, multidimensional arrays at blazingly faster speeds than Python. NumPy also features sophisticated array indexing and slicing operations, as well as broadcasting, which permits element-wise multiplication between a multi-element axis of an array and a one-element axis of an array. However, the four-layer loop makes very poor use of these properties: it uses NumPy to perform element-wise multiplication.
Each implementation in the example code requires iteration over (1) the number of training samples, (2) the output width and height of each sample (which are based on the square area of the input image), and (3) the number of filters. And yet, all of these properties are originally featured in arrays: the input to each layer, the weight matrix, etc. So it is quite feasible to operate on massive subsections of this array instead of lots of element-wise operations.
One idea is to iterate over the elements of each filter rather than the elements of each image, since the filters are smaller. Theoretically, element-wise multiplication of each element of each filter would require (f_w f_w c) iterations - in the network above: (3 3 32) = 288 iterations, which is certainly an improvement. (But this methodology is not applicable to the pooling layers.) Still - we can do better.
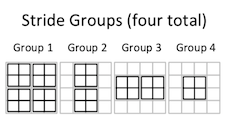
A much better idea - and the heart of the following technique - is to reorient the input into stride groups. A stride group is the set of input elements for all non-overlapping strides, assembled into a sub-matrix of elements and aligned with a corresponding element of the filter matrix with which those elements of the input are multiplied during convolution - like this:

This approach has an extremely important advantage: The number of iterations is irrespective of the size of the input, the number of input channels, and the number of filters.
In this approach, four total iterations are required whether the matrix is 4x4, or 5x5, or 100x100. Four total iterations are required whether the number of filters is 1, or 32, or 10,000. The number of iterations is strictly based on the filter width and the stride. Larger inputs and larger number of filters will increase the sizes of the matrix that are multiplied together in each iteration, but not the number of iterations.
Moreover: if the filter width and the stride are equal - for example, a 2x2 filter with a stride of 2 - then only one shift group exists... and all of convolution is performed in a single matrix multiplication. Iteration is entirely eliminated.
The redesign of the neural network architecture using stride groups is presented in cnn-numpy-sg.py, and can be used by omitting the "naive" parameter from the command:
python3 mnist.py cnn
The redesign presents identical versions of FlatLayer, FCLayer, and Network. The implementations of ConvLayer and PoolLayer are different, and not as readable, but they are functionally equivalent and can be swapped into place.
I will admit that I am a NumPy amateur. I am certain that the NumPy code could be rewritten to consolidate operations (such as broadcasting rather than repeating) and to make tremendously better use of the sophisticated capabilities of NumPy.
And yet... this amateur implementation is approximately 1,000 times faster than the naive implementation.
A one-ConvLayer CNN using the stride groups implementation can complete an entire 100-minibatch epoch over 95% of the MNIST data set in a little over two minutes (vs. 18 hours for the example code). It is performant enough to observe and experiment with its learning capabilities on the MNIST data set. It exhibits a typical classification error under 30% in one epoch, that is, having seen each of the 65,500 samples only once. Again, continued training reduces the classification error below 3%.
On the one hand, the fully-connected network performs better performance on this training set in a shorter period of time (e.g., one minute). However, the fully-connected network requires 100 epochs, raising the prospect of overtraining. And of course, fully-connected network also scales poorly to larger data sets, since the number of weights of the first FC layer is (number of neurons input size number of channels). Fully-connected networks also fail to account for localized characteristics, so they will train more slowly and may be more susceptible to extraneous noise.
This project demonstrates:
The capabilities of neural network architectures with an application for multi-class classification of the MNIST data set;
The validity of the example CNN architecture;
The computational power of NumPy when used well (and the importance of using it well!); and
An apparently novel computational technique for aligning the capabilities of NumPy with some typical neural network operations.